偽記憶
Hopfield 連想記憶は幾つかの学習パターンを記憶し、ノイズを乗せた学習パターンを与えてノイズを回復する形で利用されます。したがって、記憶容量とともにノイズ除去性能が求められます。ノイズ除去性能に深く関わってくるのが偽記憶という現象です。学習に成功すれば、学習パターンはエネルギーの極小点になります。しかし、学習パターン以外にもエネルギーの極小点は生じます。これを偽記憶と呼びます。偽記憶は連想記憶の性能に説明するために便利な概念です。私の研究でも連想記憶の高次元化モデルを提案した時に、実験結果を理論付けるために利用してきました。
典型的な偽記憶 reversed pattern
典型的な偽記憶が2種類あり、1つが reversed pattern です。\( \vec{a} \) を学習パターンとします。ヘブ則で学習すると \( W = \frac{1}{N-1} \left( \, \vec{a} \,\vec{a}^{\mathrm{T}} \,-\, E \, \right) \) となります。\( W \vec{a} = \vec{a} \) が \( \vec{a} \) を記憶している根拠になりますが、\( W ( – \, \vec{a} ) = ( – \, \vec{a} ) \) も成り立ち、\( – \, \vec{a} \) も記憶されていることになります。\( – \, \vec{a} \) を \( \vec{a} \) の reversed pattern と呼びます。
学習パターンと reversed pattern は学習済みのネットワークを見ても区別がつきません。それは \( \vec{a} \) の代わりに \( – \, \vec{a} \) を学習パターンとしても同じネットワークとなるからです。実際、\( W = \frac{1}{N-1} \left( \, ( – \vec{a} )\,( – \vec{a} )^{\mathrm{T}} \,-\, E \, \right) = \frac{1}{N-1} \left( \, \vec{a} \,\vec{a}^{\mathrm{T}} \,-\, E \, \right) \) となります。
reversed pattern はどのような問題を引き起こすのでしょうか。\( \vec{a} \) を出力すべき入力に対して \( – \,\vec{a} \) を出力してしまうようなことが起こるでしょうか。\( \pm \vec{a} \) は間反対に位置しますので、半数以上のニューロンが反転している場合に \( – \,\vec{a} \) を出力することになります。他の学習パターン \( \vec{b} \) がある場合に、 \( \vec{b} \) が \( \vec{a} \) の近くに無くても \( -\,\vec{b} \) が近くにあることはあり得なくはありません。個人的な意見ですが、無相関な学習パターンならともかく、学習パターンには \( +1 \) を多く含むなど何らかの傾向があると思われ、reversed pattern はその傾向が反転して現れますので reversed pattern の直接的な影響は少ないと思います。reversed pattern は符号による対称性が引き起こす現象です。高次元化したモデルは別の対称性をもち、これまでとは異なる偽記憶を引き起こします。それらは学習パターンの近くにも存在して、ノイズ耐性を大きく損ないます。実数値モデルで偽記憶とノイズ耐性の議論がどれくらいされているのかは知りませんが、高次元モデル間の比較ではかなり有用な根拠となりました。
典型的な偽記憶 mixture pattern
2つ目の典型的な偽記憶として mixture pattern を取り上げます。3個の学習パターン \( \vec{a}, \vec{b}, \vec{c} \) を考えます。\( \vec{a} + \vec{b} + \vec{c} \) の各成分は \( \pm 1 \) または \( \pm 3 \) になります。符号のみを取り出して \( \pm 1 \) にしたものを \( [ \, \vec{a} + \vec{b} + \vec{c} \, ] \) と表すことにします。\( [ \, \vec{a} + \vec{b} + \vec{c} \, ] \) またはその近傍に偽記憶が生じます。これを mixture pattern と呼びます。下図はエネルギーのイメージです。学習パターンに比べてエネルギーは高くなります。
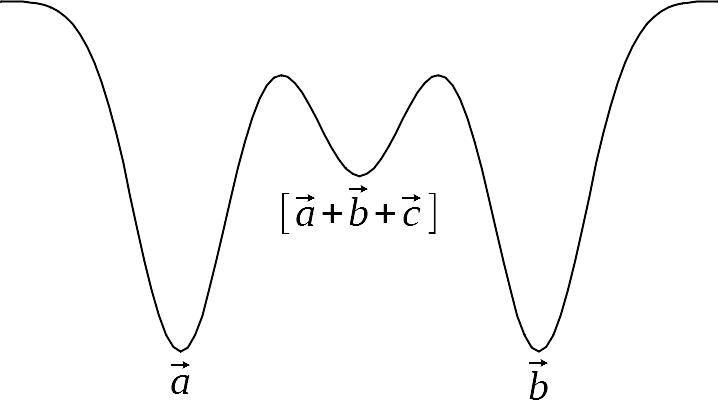
上のエネルギー図において極小となっている位置に引き込まれます。極小点を牽引子(attractor)と呼びます。谷になっている範囲を牽引皿(basin)と呼びます。エネルギーは減少するので、牽引皿に入ると牽引子に引き寄せられることになります。エネルギーの高い mixture pattern の牽引皿は小さいと予想されます。mixture pattern は2パターンの合成でも生じます。また学習パターンだけでなく、reversed pattern も mixture pattern の対象になります。mixture pattern は学習パターンまたは reversed pattern の組み合わせですから、学習パターン数が増えると爆発的に増えるでしょう。牽引皿は小さいとはいえ mixture pattern の数は膨大になりますので、捕まる危険性は高いと考えられます。