Hopfield 連想記憶

Hopfield Network の構造を与え、収束することまで証明しました。今回は Hopfield Network の応用として、連想記憶を解説します。Hopfield Network を使った連想記憶を Hopfield Associative Memory と呼び、以下では HAM と略します。

HAM

Hopfield Network はどんな初期状態からでも収束して、安定状態ではエネルギーが極小となります。ここまでの議論では安定状態が存在することしか分かりません。HAM では指定した状態が安定状態になるようにネットワークを構築します。例を考えてみましょう。ニューロン数を２５として、次の２５次元ベクトル $\overrightarrow{a}$ を考えます。

$\begin{array}{rcl}\overrightarrow{a}& =& (-1,+1,-1,+1,-1\phantom{)}\\ & & \phantom{(}+1,+1,+1,+1,+1\phantom{)}\\ & & \phantom{(}-1,+1,-1,+1,-1\phantom{)}\\ & & \phantom{(}+1,+1,+1,+1,+1\phantom{)}\\ & & \phantom{(}-1,+1,-1,+1,-1)\end{array}$

$\overrightarrow{a}$ は行ベクトルですが、意図的に５成分ごとに改行しました。理由は白黒画像と対応付けたいからです。$+1$ を ■ $-1$ を □ と対応付けると次の図になります。

□■□■□
■■■■■
□■□■□
■■■■■
□■□■□

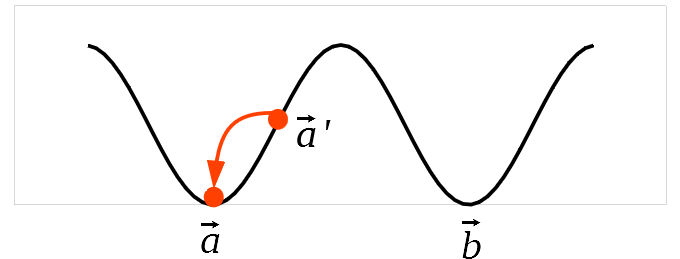
$\overrightarrow{a}$ でエネルギーが極小になるように結合荷重を定めることができれば、この図の一部を変更した図を初期値としたとき、エネルギーを減らしながら徐々に変化していき、近くにある安定状態 $\overrightarrow{a}$ に落ち着くと期待されます。今度は２ベクトル $\overrightarrow{a},\overrightarrow{b}$ を安定状態にできたと仮定しましょう。下図のように $\overrightarrow{a},\overrightarrow{b}$ のエネルギーは極小になります。$\overrightarrow{a}$ を少しだけ改変したベクトル ${\overrightarrow{a}}^{\prime }$ から始めます。このときも、最寄りの極小状態 $\overrightarrow{a}$ に引き寄せられると期待されます。HAM は単純な仕組みで自動修復できるという点が面白さの１つです。

HAMではいくつかの状態を安定させるようにネットワークを構築します。この操作を学習と呼び、安定させる状態を学習パターンと呼びます。

ヘブ則

ヘブ則は原始的で簡明な学習法です。ニューロン数を $N$ とします。状態ベクトルを行ベクトルで表現してきましたが、これ以降は列ベクトルで表現します。学習パターンを $\overrightarrow{a}=(a_1,\cdots ,a_N{)}^{\mathrm{T}}$ として、 $\overrightarrow{a}$ が安定するように HAM を構築します。$i\ne j$ に対して $w_{ij}=\frac{1}{N-1}{a}_i{a}_j$ とすると、HAM の条件 $w_{ij}=w_{ji}$ を満たします。$\overrightarrow{a}$ が安定することを確認しましょう。$\overrightarrow{a}$ を HAM に与えた時のニューロン $i$ への入力和 $S_i$ を計算します。

$\begin{array}{rcl}{S}_i& =& \sum _{j\ne i}{w}_{ij}{a}_j=\frac{1}{N-1}\sum _{j\ne i}{a}_i{a}_j{a}_j\\ & =& \frac{1}{N-1}\sum _{j\ne i}{a}_i{a}_j^2=\frac{1}{N-1}\sum _{j\ne i}{a}_i\\ & =& a_i\end{array}$

$S_i=a_i$、特に $S_i$ と $a_i$ の符号は一致し、$\overrightarrow{a}$ が安定することが分かります。ポイントとなるのが $w_{ij}{a}_j=(a_i{a}_j)a_j=a_i(a_j{a}_j)=a_i$ で結合則が重要な役割を果たします。高次元化でヘブ則を考えるとき、使用される代数が結合則を満たすことが重要になります。

結合荷重を行列を使って表現してみましょう。$W$ を $N$ 次正方行列として、$(i,j)$ 成分を $w_{ij}$ とします。現在の状態ベクトルを $\overrightarrow{x}$ としたとき、$W\overrightarrow{x}$ は列ベクトルとなり、 $i$ 成分はニューロン $i$ への入力和になります。HAM の条件は $w_{ij}=w_{ji},w_{ii}=0$ の２つがありました。それぞれ $W^{\mathrm{T}}=W,\mathrm{diag}W=O$ と書き換えられます。$W$ の対称性が HAM の安定性の根源と言えます。ヘブ則は $W=\frac{1}{N-1}\left(\overrightarrow{a}{\overrightarrow{a}}^{\mathrm{T}}\right)-\frac{1}{N-1}E$ と書き換えられます。$W\overrightarrow{a}$ も計算してみましょう。

$\begin{array}{rcl}W\overrightarrow{a}& =& \frac{1}{N-1}\overrightarrow{a}\left({\overrightarrow{a}}^{\mathrm{T}}\overrightarrow{a}\right)-\frac{1}{N-1}\overrightarrow{a}\\ & =& \frac{N}{N-1}\overrightarrow{a}-\frac{1}{N-1}\overrightarrow{a}=\overrightarrow{a}\end{array}$

行列による計算でも $W\overrightarrow{a}=\overrightarrow{a}$ という結果が得られました。これはニューロンを同時更新をしても安定することを意味していますが、同時更新では HAM の収束は保証されません。

今回の学習パターンは１つでした。次回、複数の学習パターンを扱います。

興味の対象

物理学者と工学者がこの分野を研究していますが、各々で興味の対象が異なります。工学者は連想記憶を応用することに関心があります。HAM 自体が Hopfield Network の応用の１つですが、さらに HAM に工学的応用を与えたいところです。しかし、HAM の工学的応用例は乏しいです。HAM の論文を投稿すると、HAM の応用を提示しないと納得しない査読者もいます。そういう査読者には HAM 自体がすでに応用であるという主張は通りません。これまでに HAM に関する論文が多数出版されている状況で、1査読者の価値観で否定されてしまうのはどうかと個人的には思います。そういう査読者に当たってしまったら、あきらめて別の投稿先にチャレンジするのが良いでしょう。

物理学者は統計力学のモデルとして HAM に関心があります。例えば、HAM の記憶容量は重要な問題ですが、物理学者は記憶容量を求めること自体に興味があります。私のような工学基礎の研究者は多くのパターンを記憶させたいと考えますので、記憶容量を大きくすることに関心があります。工学でも応用志向の研究者はアプリケーションに組み込みたいのでしょうが応用事例はあまりありません。