前回の学習パターンは1つでした。今回は複数パターンを学習するヘブ則を扱います。
複数パターンのヘブ則
学習パターンを \( \{ \vec{a}^p = (a_1^p, \cdots, a_N^p)^{\mathrm{T}} \,|\, p=1,2,\cdots,P \} \) とします。\( N \) はニューロン数、\(P\) は学習パターン数です。複数パターンのヘブ則は \( \displaystyle w_{ij} = \frac{1}{N-1}\sum_{p=1}^P a_i^p a_j^p \) で与えられます。1パターンのヘブ則を単純に足し合わせただけで問題はあるものの、それなりに利用されてきました。統計物理学者の研究対象としては面白いようです。\( \vec{a}^q \) が安定するか確認してみましょう。\( \vec{a}^q \) を HAM に与えた時のニューロン \(i\) への入力和は次のようになります。
\( \begin{eqnarray}
S_i^q &=& \sum_{j\neq i} w_{ij} a_j^q \\
&=& a_i^q + \frac{1}{N-1}\sum_{p\neq q}\sum_{j\neq i} a_i^p a_j^p a_j^q
\end{eqnarray} \)
最後の式に現れる2重和を crosstalk term と呼びます。1パターンのヘブ則では crosstalk term は現れませんでした。学習パターンが安定するためには \( a_i^q \) と \( S_i^q \) の符号が一致することが求められます。crosstalk term を \( \epsilon_i^q \) で表すことにします。 全ての \( i,q \) に対して、\( \epsilon_i^q \) と \( a_i^q \) の符号が同じであるか、 \( | \epsilon_i^q | < 1 \) であれば問題は生じません。パターン数 \(P\) が増えると、\( | \epsilon_i^q | < 1 \) も大きくなる傾向があり、学習に失敗する危険性も増大します。
ヘブ則の記憶容量
学習できるパターン数に限りがあり、限界値があると予想されます。この限界値を記憶容量と呼び、\(C\) で表すことにします。\(P\) を固定すると、\( \epsilon_i^q \) は \(N\) に反比例するので、記憶容量は \(N\) と共に増加します。\(N\) を固定し、\(P\) をどこまで増やせるかが問題となります。\(P\) は \(N\) に比例して増やすことができると考えられています。レプリカ法という解析手法では、\( C=0.138N \) という結果が得られています。 ただし、この評価に関する解釈には十分注意する必要があります。
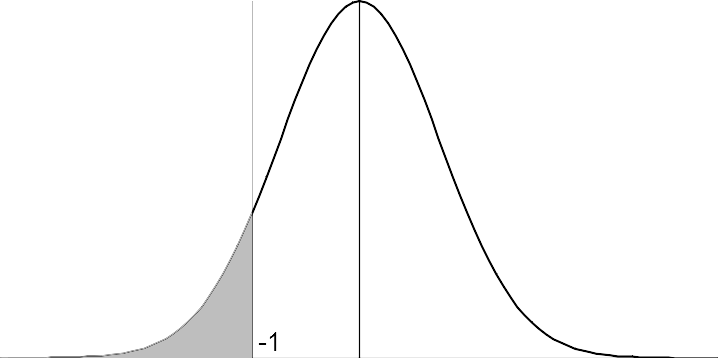
初等的な解析法は crosstalk term を正規分布で近似する方法です。\( \xi_{ij}^{pq} = a_i^p a_j^p a_j^q \) は \( \pm 1 \) をとる独立な変数と見なして、\( \displaystyle \epsilon_i^q = \frac{1}{N}\sum_{j,p} \xi_{ij}^{pq} \) を正規分布で近似することにより評価します。\( \xi_{ij}^{pq} \) は平均 0、分散 1 の確率変数で、\( \sum \xi_{ij}^{pq} \) は \(NP\) 個の独立確率変数の和と見なします。中心極限定理により、\( \frac{1}{\sqrt{NP}}\sum \xi_{ij}^{pq} \) は標準正規分布 \( N(0,1) \) で近似され、したがって \( \epsilon_i^q \) は \( N(0,\frac{P}{N}) \) と近似されます。 \( \epsilon_i^q < -1 \) となる確率が許容範囲となる \(P\) を記憶容量と考えます。許容範囲に対して \(P\) が定まり、許容範囲の設定に人の裁量が入る余地があります。
高度な解析法としてレプリカ法があります。統計物理に長けた研究者が利用する手法で、私は使いこなせません。\( \xi_{ij}^{pq} \) を独立な確率変数とみなすところは同じです。\(P\) を増やしていくと学習パターンと安定状態に相関がみられるようなのですが、ある一定の数を超えると相転移という現象が生じて相関が崩壊してしまうそうです。その結果、記憶容量は明確な数値 \( C=0.138N \) として得られます。
ヘブ則の記憶容量に関する議論は次の本が詳しいです。
Introduction To The Theory Of Neural Computation (John A. Hertz, Anders S. Krogh, Richard G. Palmer 共著)
ヘブ則の記憶容量に関する注意
記憶容量を解析する上で学習パターンがランダムに生成されているという前提条件があります。これは学習パターンが無相関を仮定しています。実際のデータに適用するときは学習パターンの間に相関があることが想定され、記憶容量は理論値よりも下がります。ちなみに、学習パターンが直交すると仮定すると crosstalk term は消滅して記憶容量は \(N\) になります。
他にも注意すべき点があります。学習パターンの数が記憶容量を下回れば、安定させることができると勘違いされがちです。ヘブ則の記憶容量の解析では、安定状態が学習パターンからずれることを許容しています。言い換えると、学習パターンの近くに安定状態があることが保証されるだけです。実際に \(10\times 10\) の2値画像(具体的には数字、アルファベットの画像やドット絵を使用します)を計算機シミュレーションで使用すると、\(N=100\) なので \( C=0.138N=13.8 \) となり、13パターンまで許容されると期待しますが、正確に記憶できるのは3パターン程度だったりします。実験を経験したことのない査読者からは \( C=0.138N \) を理由に、もっとパターン数を増やせるはずと実験の拡張を求められることもあります。もちろん、このテーマについて十分な知識をもった研究者は限られていますので仕方のないことで、査読を引き受けていただけるだけでも有難いことです。\(N\) を増やせばパターン数を増やせると思うかもしれませんが、意外と上手く行かないこともあります。今度はニューロン数が増えることで1ニューロンも間違えることなく憶えることが難しくなってしまうのです。
